CFD를 포함한 영상/이미지 처리, DSP(digital-signal processing)를 포함한 많은 전산학에서는 Parallel 상의 효과적인 iterative solver 구현을 위해서 Algebraic Multi-Grid 기법을 많이들 사용하는데, 이 기법은 각 단계별로 coarsening한 격자를 수렴시킨 후 fine한 격자로 결과를 보내고 다시 수렴시키는 기법입니다.
가장 많이 쓰이는 역 행렬 구하기 알고리즘인 Gauss-Seidel의 경우 big O notation으로 문제 크기 n에 대해 계산 시간은 O(n^2 * log n)에 비례하는 것으로 알려져 있습니다. 실제로는 어떻게 구현하느냐에 따라 차이가 있지만, 이를 multi-grid로 구현하면 계산 량이 O(n)으로 줄어드는 것으로 알려져 있습니다. Log n은 상대적으로 n^2에 비해 작기 때문에, n^2의 계산 량만큼 줄어드는 셈이라고 보면 됩니다, 만약 2차원 문제에서 격자수가 1/2이 되면 계산 속도는 4배가 됩니다. 이를 이용하여 계산이 몇 배 빠른 coarser grid 단계에서 수렴을 충분히 여러 번 시키고 finer grid로 결과를 보내면서(interpolation) iteration당 계산시간을 줄이자는 것이 multi-grid의 전략입니다.

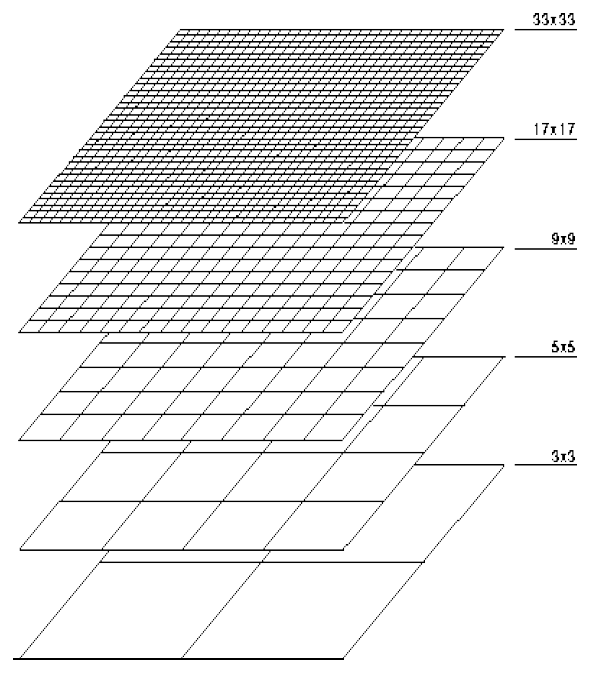
시각적으로 표현하자면 위 그림과 같습니다. (실제로 AMG는 격자level을 나누는 게 아니라 equation set의 각 coefficient matrix A_p를 모아서 만들기 때문에 완전히 같지는 않음) 여기에서 각 단계별 marching을 어떻게 할 것인가에 따라 V, W, F, Flex Cycle 등으로 나뉩니다. 각 사이클은 다음과 같이 동작합니다.
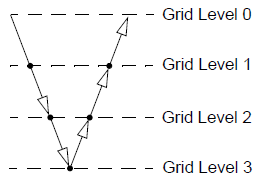
처음 보여 드린 모나리자 그림을 보면, 격자를 잘 짜더라도(항상 그런 것은 아니지만) coarsening을 너무 심하게 시키면 더 coarse한 grid level에서의 A_p값이 0에 수렴해버릴 수 있습니다. 이것이 multi-grid 기법의 단점입니다. 물론 grid level을 깊게 내려가는 가장 큰 이유는, 1) 격자의 수가 매우 많고, 2)각 level에서의 수렴성이 안 좋기 때문입니다. 이 2번이 문제인데, 정말 격자가 문제인 경우도 있고, physics set-up이 ill-posed(undetermined)한 경우로 나뉠 수 있습니다.
그럼 ill-posed 문제의 예를 들어보겠습니다. 우선 고객 혹은 엔지니어들이 가장 흔하게 하는 실수 중 하나로, outlet boundary condition을 부적절하게 주는 경우와 inverse problem을 풀려고 하는 경우입니다.
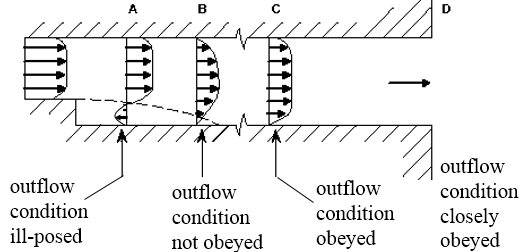
위 그림과 같이 만약 A위치에 outflow condition을 주게 된다면, reversed flow가 너무 심하여, solution이 제대로 converge하지 않을 수 있습니다. 이렇듯 잘 풀릴듯한 문제에서도 경계 조건 위치나 값에 따라 수렴되는 정도는 극과 극을 오갈 수 있습니다.
Inverse problem의 대표적인 예로, inlet-outlet에 모두 static pressure를 주는 경우를 들 수 있습니다. 입구와 출구의 압력 값만 맞다면 내부의 속도는 무엇이든 될 수 있기 때문에 속도를 결정할 수가 없습니다. 이러면 정말 아무 속도나 나올 때까지 한없이 iteration이 돌아가게 됩니다.
AMG솔버를 사용할 경우 메모리 사용량은 약 33%에서 최대 50%까지 더 소모가 되는 것으로 알려져 있습니다. 또한 coarsening 단계가 깊어질수록 MPI communication의 overhead가 커져, AMG coarsening의 장점이 상쇄되어 버리는 경우도 있을 수 있습니다. 이런 경우에는 AMG Coarsening level의 제한을 줄 수 있습니다.

Solver > (flow, energy등의 solver) > AMG Linear Solver > V, W, F Cycle에 들어가 보면 다음과 같이 Max Levels가 들어가 있습니다.
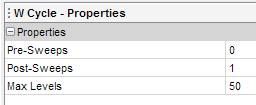
Max Levels가 기본값이 50으로 되어 있습니다. 만약 10단계에서 오류가 난다면, 해당 단계를 9 혹은 8로 줄일 수 있습니다. 계산 시간은 조금 더 걸릴 수 있으나, 수렴성은 개선할 수 있습니다.


