Design of Experiments(DOE)는 실험의 계획과 실행을 통해 특정 시스템이나 프로세스에서 변수들이 결과에 미치는 영향을 효과적으로 이해하고 분석하는 방법론입니다. 이 방법론은 통계적 기법을 사용하여 여러 입력 변수들이 결과에 미치는 영향을 분석하고, 이를 통해 시스템이나 프로세스의 성능을 최적화하는 데 도움을 줍니다.
DOE의 주요 종류
- Fully Randomized Design
모든 처리가 무작위로 할당되는 가장 기본적인 실험 설계입니다. Fully Randomized Design은 실험의 처리를 모든 실험 단위에 무작위로 할당하는 가장 간단한 형태의 실험 설계입니다. 이 방법은 실험의 결과가 처리에 의해서 만 영향을 받고, 다른 외부 요인에 의해 영향을 받지 않는 경우에 사용할 수 있습니다. 예를 들어 식물의 성장에 물의 양이 어떻게 영향을 미치는지 알아보는 실험이 있습니다. 이 경우 처리는 물의 양이 될 것이고, 실험 단위는 각각의 식물이 될 것입니다.
a. 먼저, 실험을 진행할 식물을 동일한 조건에서 성장 시킵니다. 이렇게 하면 식물 간의 차이가 실험 결과에 미치는 영향을 최소화할 수 있습니다.
b. 다음으로, 각 식물에게 주는 물의 양을 결정합니다. 예를 들어, 하루에 100ml, 200ml, 300ml의 물을 주는 세 가지 처리를 설정할 수 있습니다.
c. 이제 각 처리를 모든 식물에 무작위로 할당합니다. 예를 들어, 30개의 식물이 있다면, 각 처리를 10개의 식물에 무작위로 할당할 수 있습니다.
d. 일정 기간 동안 실험을 진행한 후, 각 식물의 성장을 측정합니다.
e. 마지막으로, 물의 양(처리)에 따라 식물의 성장(결과)이 어떻게 달라지는지 분석합니다.
이렇게 완전히 무작위화된 설계를 사용하면, 처리의 영향을 명확하게 파악할 수 있습니다. 그러나 이 방법은 외부 요인의 영향을 완전히 배제할 수 없으므로, 외부 요인의 영향을 제어해야 하는 복잡한 실험에서는 다른 설계 방법을 사용해야 할 수도 있습니다.
- 블록 설계(Block Design): 실험 단위들을 유사한 그룹(블록)으로 나누고, 각 블록 내에서 처리를 무작위로 할당하는 설계입니다. 블록 설계(Block Design)는 실험 단위들을 유사한 그룹(블록)으로 나누고, 각 블록 내에서 처리를 무작위로 할당하는 실험 설계 방법입니다. 이 방법은 외부 요인의 영향을 제어하고, 처리의 효과를 더 명확하게 파악하는 데 도움이 됩니다.
예를 들어, 서로 다른 품종의 씨앗에 서로 다른 비료를 사용하여 어떤 비료가 가장 좋은 성장을 촉진하는지 알아보려는 실험을 생각해봅시다. 이 경우, 처리는 비료의 종류가 될 것이고, 블록은 씨앗의 품종이 될 것입니다.
a. 먼저, 실험을 진행할 씨앗을 선택합니다. 예를 들어, A, B, C 세 가지 품종의 씨앗을 사용한다고 가정해봅시다.
b. 다음으로, 각 씨앗에게 줄 비료를 결정합니다. 예를 들어, 1, 2, 3의 세 가지 비료를 사용한다고 가정해봅시다.
c. 이제 각 품종의 씨앗(블록)에 대해 각 비료(처리)를 무작위로 할당합니다. 예를 들어, A 품종의 씨앗에는 1, 2, 3의 비료를 각각 무작위로 할당하고, B 품종, C 품종에 대해서도 마찬가지로 진행합니다.
d. 일정 기간 동안 실험을 진행한 후, 각 씨앗의 성장을 측정합니다.
e. 마지막으로, 각 품종에 대해 어떤 비료가 가장 좋은 성장을 촉진하는지 분석합니다.
이렇게 블록 설계를 사용하면, 품종과 같은 외부 요인의 영향을 제어하고, 비료의 효과를 더 명확하게 파악할 수 있습니다. 그러나 이 방법은 블록을 정의하고, 각 블록 내에서 처리를 무작위로 할당하는 과정이 필요하므로, 완전히 무작위화된 설계보다는 약간 복잡합니다. - 요인설계(Factorial Design): 두 개 이상의 요인이 결과에 미치는 영향을 동시에 조사하는 실험 설계입니다. 이 설계는 요인 간의 상호작용도 고려할 수 있습니다.
예를 들어, 식물의 성장에 물의 양과 비료의 종류가 어떻게 영향을 미치는지 알아보고자 하는 실험을 생각해봅시다. 이 경우, 요인은 물의 양과 비료의 종류가 될 것이고, 실험 단위는 각각의 식물이 될 것입니다.
a. 먼저, 실험을 진행할 식물을 동일한 조건에서 성장시킵니다. 이렇게 하면 식물 간의 차이가 실험 결과에 미치는 영향을 최소화할 수 있습니다.
b. 다음으로, 각 식물에게 주는 물의 양과 비료의 종류를 결정합니다. 예를 들어, 하루에 100ml, 200ml의 물을 주는 두 가지 처리와, 1, 2, 3의 세 가지 비료를 사용한다고 가정해봅시다.
c. 이제 각 처리의 조합을 모든 식물에 무작위로 할당합니다. 예를 들어, 30개의 식물이 있다면, 각 처리의 조합(100ml & 비료 1, 100ml & 비료 2, …, 200ml & 비료 3)을 5개의 식물에 무작위로 할당할 수 있습니다.
d. 일정 기간 동안 실험을 진행한 후, 각 식물의 성장을 측정합니다.
e. 마지막으로, 물의 양과 비료의 종류(요인)에 따라 식물의 성장(결과)이 어떻게 달라지는지, 그리고 물의 양과 비료의 종류가 서로 상호작용하여 식물의 성장에 어떤 영향을 미치는지 분석합니다.
이렇게 요인설계를 사용하면, 여러 요인과 그들의 상호작용이 결과에 미치는 영향을 동시에 파악할 수 있습니다. 그러나 이 방법은 여러 요인과 그들의 조합을 고려해야 하므로, 다른 설계 방법보다는 더 복잡하고 많은 실험 단위가 필요할 수 있습니다. - 중심합성설계(Central Composite Design): 반응 표면 방법론에서 사용되는 설계로, 요인의 수준을 다양하게 조절하여 반응 표면을 추정하는 데 사용됩니다. 중심합성설계(Central Composite Design, CCD)는 반응 표면 방법론(Response Surface Methodology, RSM)에서 사용되는 실험 설계 방법입니다. 이 방법은 요인의 수준을 다양하게 조절하여 반응 표면을 추정하는 데 사용됩니다. 중심합성설계는 세 가지 부분으로 구성됩니다:
- 요인설계(Factorial Design): 두 개 이상의 요인이 결과에 미치는 영향을 동시에 조사합니다.중심점(Center Points): 실험 영역의 중심에서 여러 번 반복되는 실험입니다. 이를 통해 실험의 변동성을 추정하고, 곡률 효과를 확인할 수 있습니다.별점점(Star Points): 실험 영역을 벗어나는 요인의 수준입니다. 이를 통해 반응 표면의 곡률을 추정할 수 있습니다.
예를 들어, 두 가지 요인 (온도와 압력)이 화학 반응의 수율에 어떻게 영향을 미치는지 알아보려는 실험을 생각해봅시다. 이 경우, 요인은 온도와 압력이 될 것이고, 실험 단위는 각각의 화학 반응이 될 것입니다.
a. 먼저, 실험을 진행할 온도와 압력의 범위를 결정합니다. 예를 들어, 온도는 50℃에서 150℃, 압력은 1atm에서 5atm으로 설정할 수 있습니다.
b. 다음으로, 이 범위 내에서 요인설계를 수행합니다. 예를 들어, (50℃, 1atm), (50℃, 5atm), (150℃, 1atm), (150℃, 5atm)의 네 가지 조합을 실험할 수 있습니다.
c. 이제 중심점을 추가합니다. 이 경우, 중심점은 (100℃, 3atm)이 될 것입니다. 이 중심점에서 여러 번 실험을 반복하여 변동성을 추정하고, 곡률 효과를 확인합니다.
d. 마지막으로, 별점점을 추가합니다. 이 경우, 별점점은 실험 영역을 벗어나는 온도와 압력의 수준이 될 것입니다. 이를 통해 반응 표면의 곡률을 추정할 수 있습니다.
e. 일정 기간 동안 실험을 진행한 후, 각 조건에서의 화학 반응의 수율을 측정합니다.
f. 마지막으로, 온도와 압력(요인)에 따라 화학 반응의 수율(결과)이 어떻게 달라지는지, 그리고 온도와 압력이 서로 상호작용하여 화학 반응에 어떤 영향을 미치는지 분석합니다.
이렇게 중심합성설계를 사용하면, 여러 요인과 그들의 상호작용이 결과에 미치는 영향을 동시에 파악할 수 있습니다. 또한, 요인의 수준을 다양하게 조절하여 반응 표면을 추정할 수 있습니다. 그러나 이 방법은 여러 요인과 그들의 조합을 고려해야 하므로, 다른 설계 방법보다는 더 복잡하고 많은 실험 단위가 필요할 수 있습니다. - 라틴스퀘어 설계(Latin Square Design): 두 개의 블록 요인을 동시에 제어하는 실험 설계입니다. 이 방법은 특히 두 가지 외부 요인이 결과에 영향을 미칠 때 유용합니다.
예를 들어, 식물의 성장에 물의 양이 어떻게 영향을 미치는지 알아보려는 실험을 생각해봅시다. 이 경우, 처리는 물의 양이 될 것이고, 블록은 식물의 위치와 식물의 품종이 될 것입니다.
a. 먼저, 실험을 진행할 식물을 선택합니다. 예를 들어, A, B, C 세 가지 품종의 식물을 사용한다고 가정해봅시다.
b. 다음으로, 각 식물에게 줄 물의 양을 결정합니다. 예를 들어, 하루에 100ml, 200ml, 300ml의 물을 주는 세 가지 처리를 설정할 수 있습니다.
c. 이제 각 품종의 식물(블록)과 각 위치(블록)에 대해 각 물의 양(처리)를 무작위로 할당합니다. 이 때, 각 행과 각 열에서 모든 처리가 한 번씩만 나타나도록 합니다. 이렇게 하면 위치와 품종에 따른 변동을 제어할 수 있습니다.
d. 일정 기간 동안 실험을 진행한 후, 각 식물의 성장을 측정합니다.
e. 마지막으로, 물의 양(처리)에 따라 식물의 성장(결과)이 어떻게 달라지는지 분석합니다.
이렇게 라틴스퀘어 설계를 사용하면, 위치와 품종과 같은 두 가지 외부 요인의 영향을 동시에 제어하고, 물의 양의 효과를 더 명확하게 파악할 수 있습니다. 그러나 이 방법은 블록을 정의하고, 각 블록 내에서 처리를 무작위로 할당하는 과정이 필요하므로, 완전히 무작위화된 설계나 블록 설계보다는 더 복잡합니다.
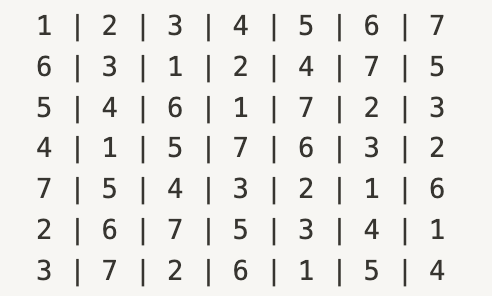
라틴 스퀘어(Latin Square)는 행과 열에서 각 요소가 한 번씩만 나타나는 n x n 배열입니다. 이는 실험 설계에서 두 가지 외부 요인의 영향을 제어하는 데 사용됩니다.
아래 그림은 7×7 라틴 스퀘어를 그림으로 표현한 것이다. 이 배열에서 각 숫자는 처리를 나타내고, 각 행과 열은 블록(외부 요인)을 나타냅니다. 이렇게 하면 각 처리가 각 블록에서 한 번씩만 나타나므로, 두 가지 외부 요인의 영향을 동시에 제어할 수 있습니다. 라틴 스퀘어 설계에서는 이러한 배열을 사용하여 실험 단위에 처리를 할당합니다. 그런 다음 실험을 진행하고, 처리에 따른 결과를 분석하여 처리의 효과를 파악합니다.