전산유체역학 소개
전산 유체 역학(CFD, Computational fluid dynamics)은 유체 현상을 기술한 비선형계 편미분방정식인 나비에-스토크스 방정식(Navier-Stokes Equations)을 유한차분법 (Finite Difference Method), 유한요소법 (Finite Element Method), 유한체적법(Finite Volume Method) 등의 방법들을 사용하여 이산화하여 대수 방정식으로 변환하고, 이를 수치 기법(numerical methods)의 알고리즘을 사용하여 유체 유동 문제를 풀고 해석하는 것이다. 컴퓨터를 사용하여 공학 문제에서 유체와 기체의 상호작용을 시뮬레이션한다. 그러나, 식을 여러 가정을 통해 간단히 하거나 슈퍼컴퓨터를 사용한다 하더라도, 대부분 근사해만을 얻을 수 있다. 적용 모델이 실제에 더욱 가까울수록 아음속이나 난류 문제와 같은 복잡한 현상의 시뮬레이션이 보다 정교해진다. 코드의 검증은 실험을 수행하여 얻은 정량적 정성적 데이터와 그 오차를 비교하여 이루어진다. 전산 유체 역학은 단상 및 다상 유동(single- and multi-phase flow), 연소(combustion) 및 화학 반응(chemical reaction) 등 다양한 문제들을 해석할 수 있도록 개발되고 있다.
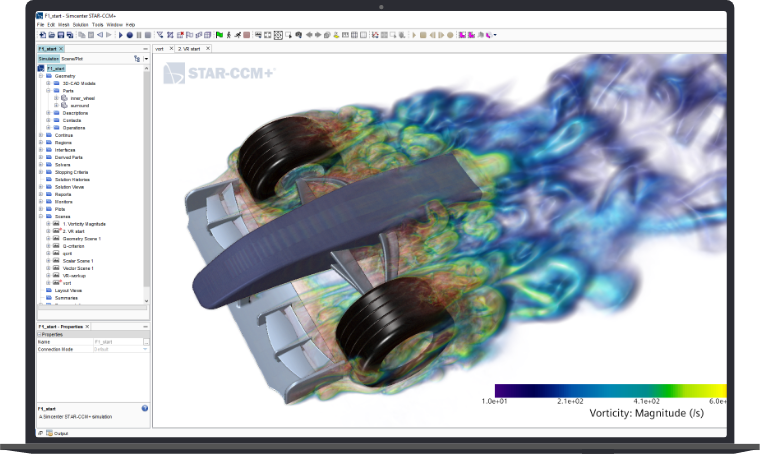
전산유체역학의 계산 방법
전산 유체 역학에 있어서 가장 기본적인 고려사항은 연속체로 가정한 유체 입자 집합들을 어떻게 컴퓨터 상에서 계산이 가능하도록 이산화 할 수 있는가이다. 그 중 하나는 공간 도메인(spatial domain)을 매우 작은 공간 격자(volume mesh or grid)로 이산화하고, 각각의 격자에 대해 운동 방정식을 세워 적절한 수치 알고리즘을 이용하여 계산하는 것이다(비점성 유동에서의 오일러 방정식이나 점성 유동에서의 나비에-스토크스 방정식). 추가적으로 이산화된 격자는 일정할 수도 있고 일정하지 않을 수도 있다(2차원의 경우 2차원에서 삼각형 격자나 3차원에서 피라미드 격자를 들 수 있음. 격자의 i, j, k 색인화(indexing)가 가능하며, 실제 격자 노드의 좌표와 논리적인 격자(logical representative grid)간의 1:1 사상(mapping)이 가능한 경우 정렬 격자계(structured grid)라고 하며, 그렇지 않은 경우 비정렬 격자계(unstructured grid)라고 함). 따라서 각각의 격자를 구분하기 위해서는 서로 다른 저장 공간(대표적으로 시스템상의 메모리)에 위치해야 한다. 만약 충격파나 불연속한 곳이 있을 경우, Gibbs 현상(Gibbs Phenomenon)이라 불리는 해석 결과의 진동을 막기 위해서는 총 변화 억제 (TVD; Total Variation Diminishing)나, 유속 수정 수송 (FCT; Flux Corrected Transport), 비진동 (ENO; Essentially NonOscillatory) 혹은 MUSCL (Monotone Upstream-centered Schemes for Conservation Laws)과 같은 고차항 계산이 가능한(혹은 고해상의) scheme이 필요하다.
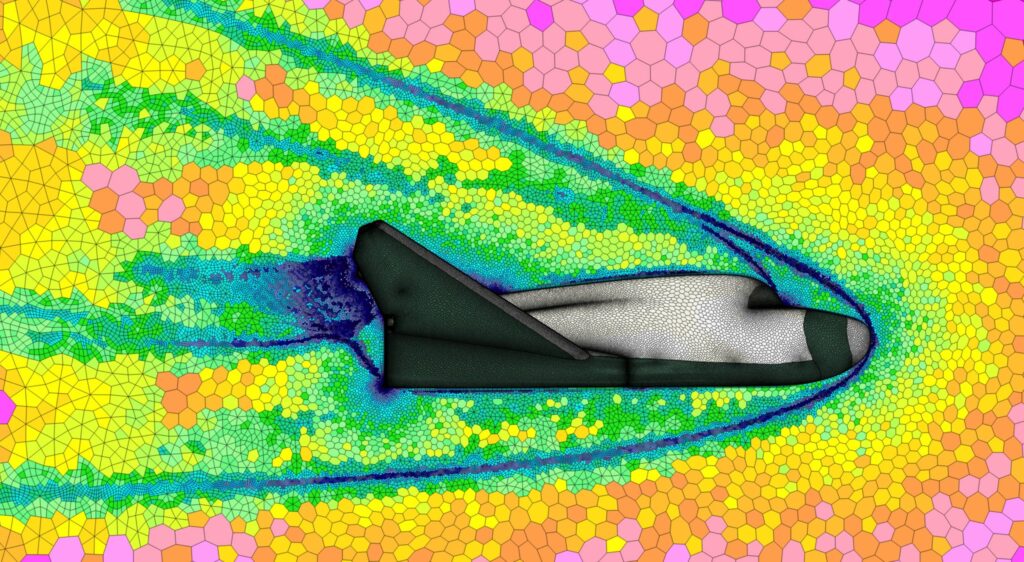
전산 유체 역학에는 격자를 이용하여 계산하지 않는 다양한 방식 또한 존재한다. 대표적으로 Smoothed particle hydrodynamics (SPH)나 유체 역학적인 문제들을 풀기위한 라그랑지언 기법(Lagrangian method), 체비쇼프 다항식이나 구면 조화 함수를 기저 함수(basis function)로 두고 지배 방정식을 투영(projection)하여 계산하는 Spectral methods, 실제 문제를 미소한 격자나 하나의 큰 계가 아니라 데카르트 격자계에 존재하는 중간 크기(mesoscopic)의 계로 등가하여 계산하는 격자볼츠만기법(LBM)등이 그것이다.

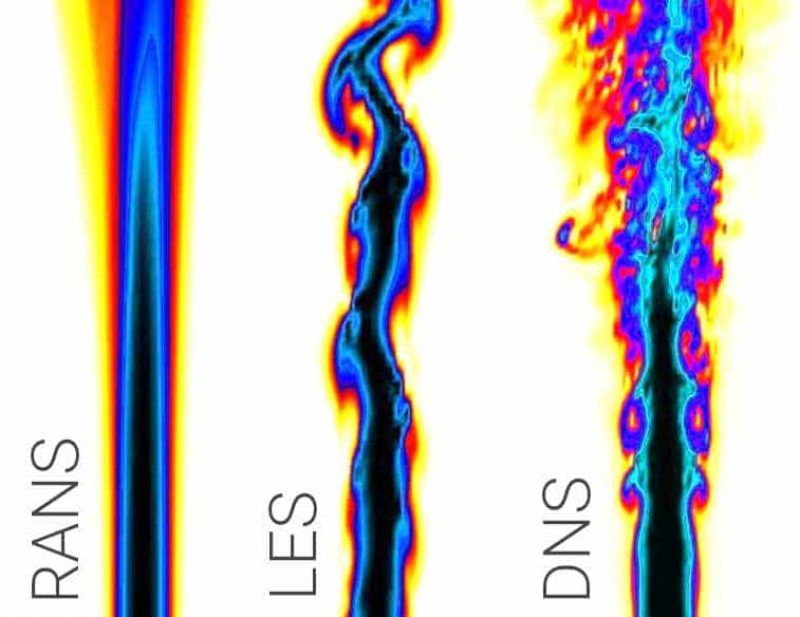
일반적으로 전산 유체 역학에서 나비에-스토크스 방정식을 풀기 위해 직접 수치 모사(Direct Numerical Simulation, DNS)와 같이 모든 난류 길이 척도(turbulent length scale)에 대한 해상도를 가진 격자를 이용하거나, 층류 유동일 경우에는 나비에-스토크스 방정식을 단순화하여 직접 계산하기도 한다. 그러나 일반적으로 모든 난류 길이 척도에 대한 해상도를 가진 격자를 계산하는 것은 현존하는 가장 고성능의 컴퓨터를 사용한다 하더라도 매우 어려운 일이다. 이런 경우 난류 유동을 모사하기 위해 난류 모델(turbulent model)이라는 것을 도입하게 된다. 난류 모델에는 DES (Detached Eddy Simulations), LES (Large Eddy Simulations), k-ε 모델, k-ω 모델, 레이놀즈 응력 모델 (RSM; Reynolds Stress Model)과 같은 RANS (Reynolds-averged Navier-Stokes)에 기반한 방정식들이 있다. 이들 난류 모델은 기본적으로 난류 전단 응력과 유동 특성간의 선형 함수 관계를 가정한 Boussinesq 가정(Boussinesq hypothesis)에 기반을 두고 있다. 여기에는 와점성 (Eddy Viscosity)을 나타내는 항인 µ_t가 매우 중요하다. 이를 와점성 모델 (EVM, Eddy Viscosity Model)이라고 한다. 와점성 모델의 단점은 해석하려는 문제에 따라 적합한 난류 모델이 사용되지 않는다면, 그 결과가 실제와 매우 큰 차이를 보이거나 물리적으로 불가능한 유동 현상을 예측할 가능성이 있다는 것이다. 그러나 Boussinesq 가정이 가지는 명쾌함과 단순성 그리고 많은 실제 유동 문제에 대해 비교적 성공적인 예측 결과를 보여 왔다는 점으로 인해 와점성 모델은 매우 유용하다. 또한 와점성 모델은 난류 전단 응력을 계산하는 데 있어서 다른 모델에 비해 상대적으로 계산 비용이 적게 든다는 장점을 가지고 있다. 이런 다양한 장점들로 인해 현재 상용으로 판매되는 대부분의 전산 유체 역학 프로그램들은 와점성 모델 및 RANS 기반의 코드로 이루어져 있다.
많은 경우, 나비에-스토크스 방정식을 다른 방정식들과 동시에 풀 수 있다. 여기에 들어가는 방정식으로는 질량 전달 (mass transfer or species concentration), 화학 반응 (chemical reactions), 열 전달(heat transfer), 공력 소음(Aero-acoustic) 등이 있다. 고도로 진보된 전산 유체 역학 코드는 혈액과 같은 비뉴턴 유체(non-Newtonian fluids)는 물론 연소와 같은 화학 반응이 일어나는 유동까지 해석이 가능하다.
https://www.youtube.com/embed/b6wfODEp0VE?feature=oembedCombustion reaction simulation by Alto EC